Example 3 Evaluate (i) (𝑙𝑖𝑚)┬(𝑥→1) (𝑥 15 − 1)/(𝑥10 − 1) (𝑙𝑖𝑚)┬(𝑥→1) (𝑥 15 − 1)/(𝑥10 − 1) = (〖(1)〗^15 − 1Lim x → ∞ x 2 x = 1 Für x gegen ∞ strebt der Graph der Funktion gegen 1 Grenzwert für x gegen − ∞ berechnen Wenn die x Werte immer kleiner werden, x − 1 − 10 − 100 − 1000 − f ( x) − 1 0, 8 0, 98 0,998 0,999 8 nähern sich die y Werte der 1 an, d h lim x → − ∞ x 2 x = 1We can also use LHR instead of series expansion for logs and this will require two applications of LHR to get the following expression L = e 6 ⋅ lim x → 0 1 x ( − 1 ( 1 x) 2 4 − x ( 2 − x) 2) = e 6 ⋅ lim x → 0 1 x ( 4 − x) ( 1 x) 2 − ( 2 − x) 2 ( 1 x) 2 ( 2 − x) 2 = e 6 ⋅ lim x → 0 1 x x ( 11 x − x
L Hopital S Rule Evaluating Limits Of Indeterminate Forms Owlcation
Lim x- 0 (1/x)^sinx
Lim x- 0 (1/x)^sinx-Lim x→x0 f′(x) g′(x) = ±∞, so gilt mit der Regel von de l'Hospital lim x→x0 f(x) g(x) = lim x→x0 f′(x) g′(x) = ±∞ • Wir betrachten nun uneigentliche Grenzwerte der Form lim x→∞ f(x) g(x) und lim x→−∞ f(x) g(x) Analysis I TUHH, Winter 06/07 Armin Iske 0If either limit does not exist, then neither limit How do we calculate the Right and Left Hand Limit of 1/x?




Lim Xrarr0 1 X N 1 X Is Equal To
Click here👆to get an answer to your question ️ Show that x→0 e^1/x 1e^1/x 1 does not exist Lim x0 (root of(1x))1/x Share with your friends Share 0 lim x → 0 1 x So there is this question in my text book which is rather more puzzling for me than I would like it to be The question is> Show that Lt x>0 e1/x1 / e1/x1 Now, The question is e1/h is infinity or undefined as h is 0 afaik And any 1 or 1 to undefined remains undefined However
X"0 1 x 1 = 1 1 = 1 (9) lim x#0 g 4(x) = lim x#0 x3 x4 x3 = lim x#0 1 x 1 = 1 1 = 1 (10) Der linksseitige und der rechtsseitige Grenzwert stimmen nicht uberein und deswegen kann die Funktion auch nicht stetig fortgesetzt werden 11 Mehr Stetigkeit Zeigen sie das f(x) = (sin(1 x) x6= 0 0 sonst nicht stetig bei null ist L osungClick here👆to get an answer to your question ️ Evaluate x→0 (tanx/x)^1/x^3 Join / Login > 11th > Applied Mathematics > Limits and Continuity > Methods of evaluating limit of a function Evaluate x → 0 lim (x tan x ) 1 / x 3 A Hence, L'Hopital's rule applies ∴ lim x→0 (1 x)n − 1 x = lim x→0 d dx((1 x)n −1) d dx(x) = lim x→0 n(1 x)n−1 ×1 −0 1 Power rule and chain rule = lim
1 Explanation x lo g (1 x) = lo g (1 x) x 1 so x → 0 lim x lo g (1 x) = x → 0 lim lo g (1 x) x 1 = lo g (x → 0 lim (1 x) x 1 ) = lo g (e) = 1 Limit \lim_{x \to 1} \frac{\log{x}}{xDemonstração do Limite Fundamental lim(x→0) (e^x 1)/ x para a galera da UFPB e de todo o Brasil Dúvdas?What is Lim x→0 ((√(1x)√(1x)) /x)?



How To Solve Lim X 0 1 X 1 X 2 E 1 X Quora
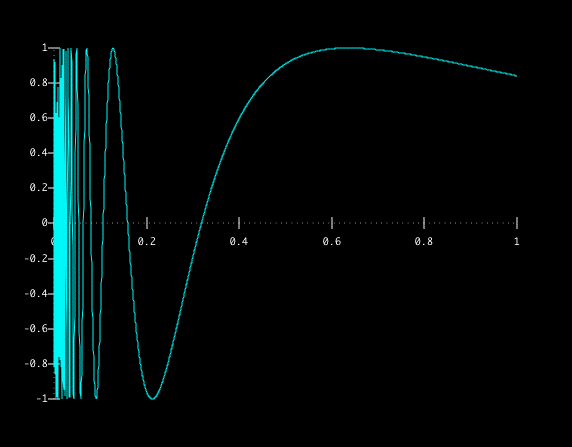



Sin 1 X And X Sin 1 X Limit Examples
Comenta aqui Valeu!Visite nosso blog http//vila when x = 0001 > lim becomes 1/0001 = 1000 so the lim approaches ∞ Thus the lim x→0 (1/x) doesn't exist, because you get a different value when you approach from the right side than you do when you approach from the left sideThis is of the type 1 to the power infinity Let the limit be A Now take ln of both sides ln(cos(x)^(1/x^2) ) = 1/x^2 times ln(cos x) when x→0 , cos 0 → 1 , so ln 1 → 0 and the bottom →0 , So we can apply D La Hospital Rule ln(A) = x→0 (1/cosx)* (



Sage Calculus Tutorial One Sided Limits




Evaluate Lim X 0 1 Cosx Cos2x 1 2 X 2 Maths Limits And Derivatives Meritnation Com
Lim (1/x, x>0) WolframAlpha Rocket science? 0 If you are not allowed to use Taylor's series, we can assume that the limits as exists and show by algebraic manipulation that they are equal to and Then we can use these results to find the limit, indeed Refer also toWhen we write things like lim x → a h (x) = lim x → a H (x) we usually mean "if either limit exists, then they both do and they are equal;




Lim X Rightarrow 1 X X 1 1 Ln X Lim X Chegg Com




L Hopital S Rule Wikipedia
Evaluate limit as x approaches 0 of (2^x1)/x Take the limit of each term Tap for more steps Apply L'Hospital's rule Tap for more steps Evaluate the limit of the numerator and the limit of the denominator Tap for more steps Take the limit of the numerator and the limit of the denominatorVerhalten im Unendlichen Für lim x!1 f(x) und lim x!1 f(x) sagt man auch Verhalten im Unendlichen Es wird nämlich untersucht, wohin der Funktionsgraph für sehr kleine undLearn how to solve limits of exponential functions problems step by step online Find the limit (x)>(0)lim((e^xx)^(1/x)) Rewrite the limit using the identity a^x=e^{x\ln\left(a\right)} Multiplying the fraction by \ln\left(e^xx\right) Apply the power rule of limits \displaystyle{\lim_{x\to a}f(x)^{g(x)} = \lim_{x\to a}f(x)^{\displaystyle\lim_{x\to a}g(x)}}
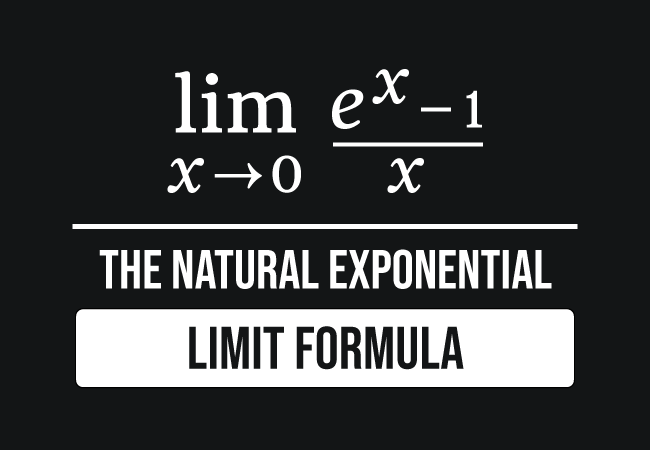



Lim X 0 E X 1 X Formula




Prove That Lim X Gt 0 Log 1 X X 1 It S Urgent Please Help Brainly In
For x > 0, lim (x→0) (sinx)^1/x (1/x)^sinx) is (a) 0 (b) –1 (c) 1 Sarthaks eConnect Largest Online Education Community For x > 0, lim (x→0) (sinx)1/x (1/x)sinx) is (a) 0 (b) –1 (c) 1 (d) 2 Login Remember Register TestEvaluate limit as x approaches 0 of 1/xcot (x) lim x→0 1 x − cot (x) lim x → 0 1 x cot ( x) Consider the left sided limit lim x→0− 1 x −cot(x) lim x → 0 1 x cot ( x) Make a table to show the behavior of the function 1 x −cot(x) 1 x cot ( x) as x x approaches 0 0 from the leftAd by Elated Stories Seniors using loophole to save for retirement When it comes to building your nest egg, you have more options than you may think Learn More 6 Answers Shaswoto Datta, studied at Studying in IIEST




What Is The Limit Of Ln X 1 X When X Approaches 0 Quora
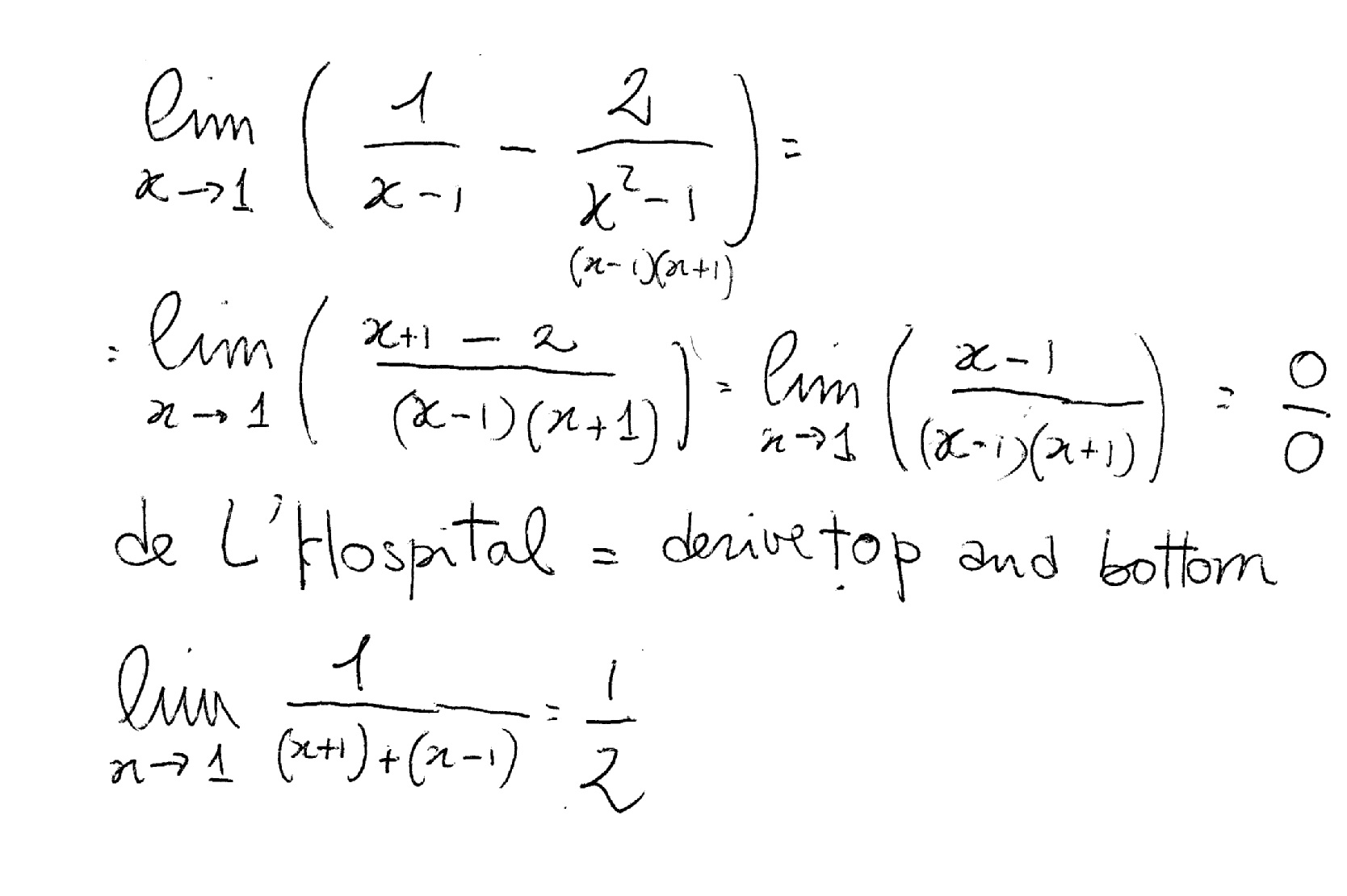



What Is The Limit Of 1 X 1 2 X 2 1 As X Approaches 1 Socratic
The limits involving infinity are considered as special ways in which a (genuine) limit fails to exist Zondrina hasn't written a proof, but Zondrina's post does show how one "worksLim x→x0 (λ·f(x)) = λlim x→x0 f(x) • F¨ur Produkte von reellwertigen (komplexwertigen) Funktionen gi lt lim x→x0 (f(x)·g(x)) = lim x→x0 f(x) lim x→x0 g(x) • F¨ur vektorwertige Funktionen f R → Rn (oder Cn) gilt lim x→x0 (f1(x),,fn(x)) = lim x→x0 f1(x),, lim x→x0 fn(x) Analysis I TUHH, Winter 06/07 Armin Iske 133We are going to show the following equality Firt of all, we definie u(x) = (1x)1 x u ( x) = ( 1 x) 1 x Two possibilities to find this limit First L'Hôpital's rule ( 1 x), g(x) = x g ( x) = x Which gives




Lim Xrarr0 1 X N 1 X Is Equal To




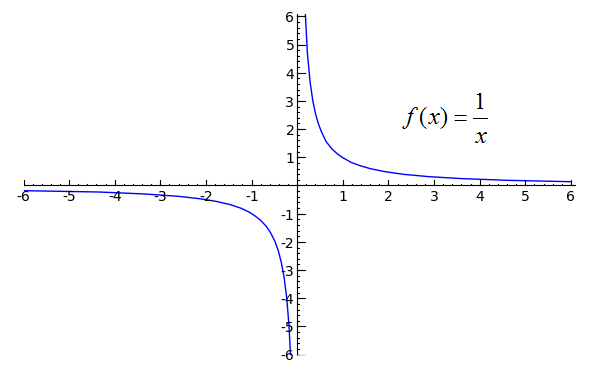
Show That Lim X 0 1 X Does Not Exist
But the circumlocution gets tiresome after a while Why does L'Hˆopital's Rule work in these "infinite" cases? We say "The limit of 1/x as x approaches 0 from the right is infinity", but we also say "The limit of 1/x as x approaches 0 from the right does not exist "! An important limit to know with a few tricky steps Follow our stepbystep solution to (cos(x) 1) / x to get a good understanding



How To Evaluate The Limit Of 1 1 X X As X Approaches 0 Quora



Efisd Net Common Pages Displayfile Aspx Itemid
Check here stepbystep solution of 'lim_x→0 (a^x x) 1/x' question at Instasolv!X p 1x 2 und skizzieren Sie den Graphen L osung lim x!0 f(x) = lim x!0 1 x p 1 x 2 = lim x!0 1 p x2 1 = 1 lim x!0 f(x) = lim x!0 1 p x 2 p 1 = lim x!0 1 p x2 1 = 1 lim x!1 f(x) = lim x!1 1 p x2 1 = 0, da p 1 x2 >jxj 2 Grenzwerte II Bestimmen Sie, wenn m oglich, die folgenden Grenzwerte (a) lim x!3 3x 9 x2 9 (b) lim x!(c) Es gilt lim x→ π 2 ln(π2 −x) tanx 0 = lim0 x→ 2 µ −1 π 2 −x ·cos2 x 0 = lim0 x→π 2 2cosxsinx −1 = 0 (d) Hier ist lim x→0 xtanx = lim x→0 etanxlnx = exlim →0 (tanxlnx) Die letzte Umformung ist wegen der Stetigkeit der Exponentialfunktion m¨oglich
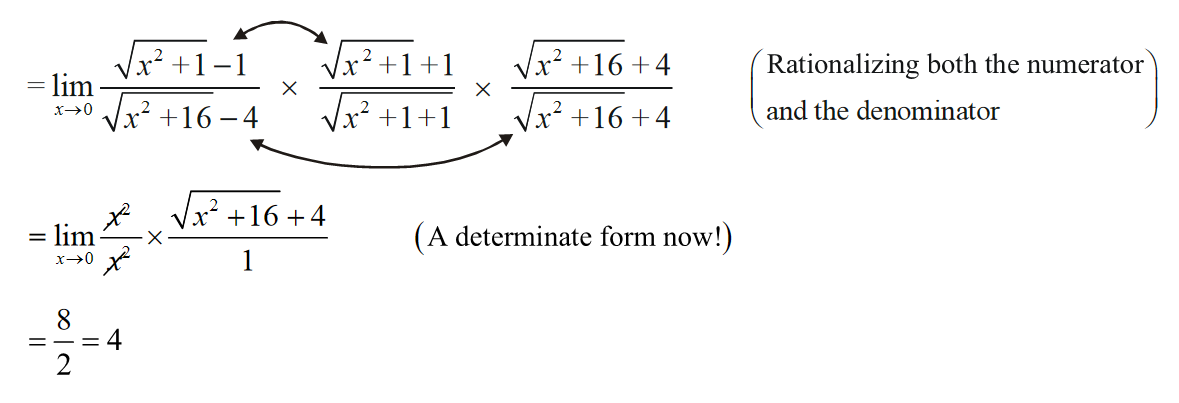



Techniques Of Evaluating Limits What Is Techniques Of Evaluating Limits Examples Solutions Cuemath




Limit Of Trigonometric Function By Substitution Lim X 1 Cos Px 2 1 X Youtube
The limit of this exponential function can be written simply in the following mathematical form by the natural logarithmic system ∴ lim x → 0 a x − 1 x = ln a Therefore, it's proved that the limit of ratio of difference of x th power of a and 1 to x as x tends to 0 is equal to natural logarithm of a Get an answer for 'lim x> 0 (cotx 1/x ) Find the limit using L'Hospital's Rule where appropriate If L'Hospital's Rule does not apply, explain why ? How to prove that limit of lim (1x)^ (1/x)=e as x approaches 0 ?



3
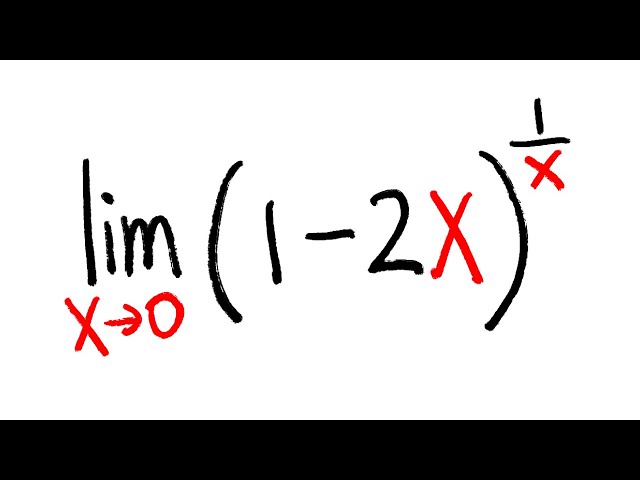



Limit Of 1 2x 1 X As X Goes To 0 L Hospital S Rule Youtube
Answer to Evaluate the following limit \lim_{x \rightarrow 0} \frac {\sqrt{1 x^2} 1}{x} By signing up, you'll get thousands of stepbystepLim x> 0 (cotx 1/xExcept that 0instead of the indeterminate 0form 0 we instead have ∞ As before, we use the exponential and natural log functions to rephrase the problem 1/x ln x 1 /x ln x x = e = e x Thus, lim x 1/x ln= lim e x x Since the function et is continuous, x→∞ x→∞ ln x ln x lim e x = e lim x→∞ x x→∞ ln x




Solution Evaluate Lim X 0 1 Cos X X 2
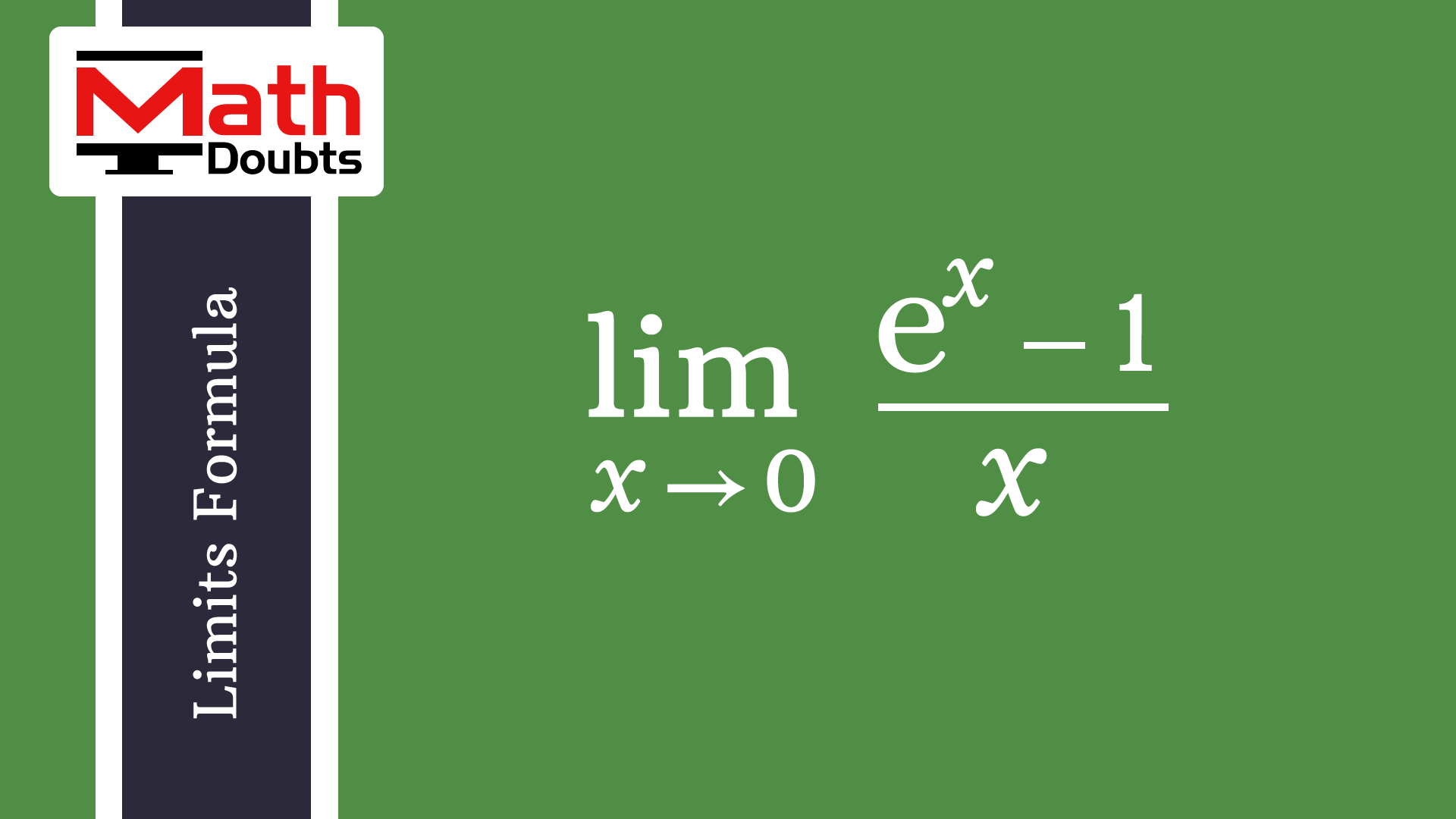



Lim X 0 E X 1 X Formula
Answer to Evaluate lim x> 0 (1sin(2x))^(1/x) By signing up, you'll get thousands of stepbystep solutions to your homework questions You canLim x→0±0 f 1(x) → ∞ lim x→1−0 f 1(x) = π 2 lim x→10 f 1(x) = − π 2 Somit ist die Funktion nicht stetig fortsetzbar (b) f 2 x → ln ln(1x2) L¨osungshinweisehierzu Die lnFunktionistdefiniertf¨uralle x > 0,strengmonoton steigend und gr¨oßer oder gleich 0 f¨ur alle x ≧ 1 Fassen wir diese beiben AussagenLim (x^31)/(x1), x>1 First we try to solve the function by substituting x with 1 then, lim (1^3 1)/(11)= 0/0 0/0 means that this method has failed because 1 is a root for both upper and
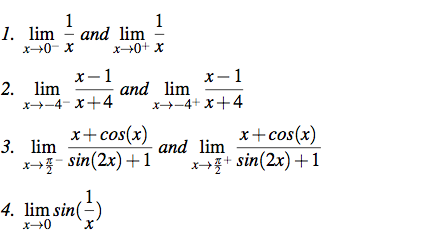



Evaluate Each Of The Following Limits 1 Lim X Chegg Com
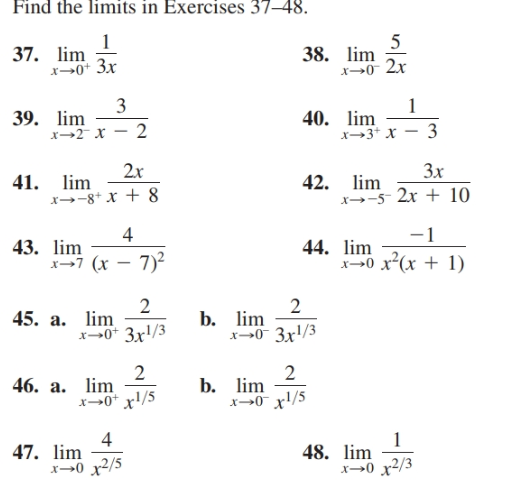



Answered Find The Limits In Exercises 37 48 5 Bartleby
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition lim x>0 (x*sin(1/x))=0 es gilt immer 1 ≤ sin(1/x) ≤ 1 also x ≤ x * sin(1/x) ≤ x und weil x und x mit x gegen 0 beide gegen 0 gehen, geht das dazwischen auch gegen 0Not a problem Unlock StepbyStep Extended Keyboard
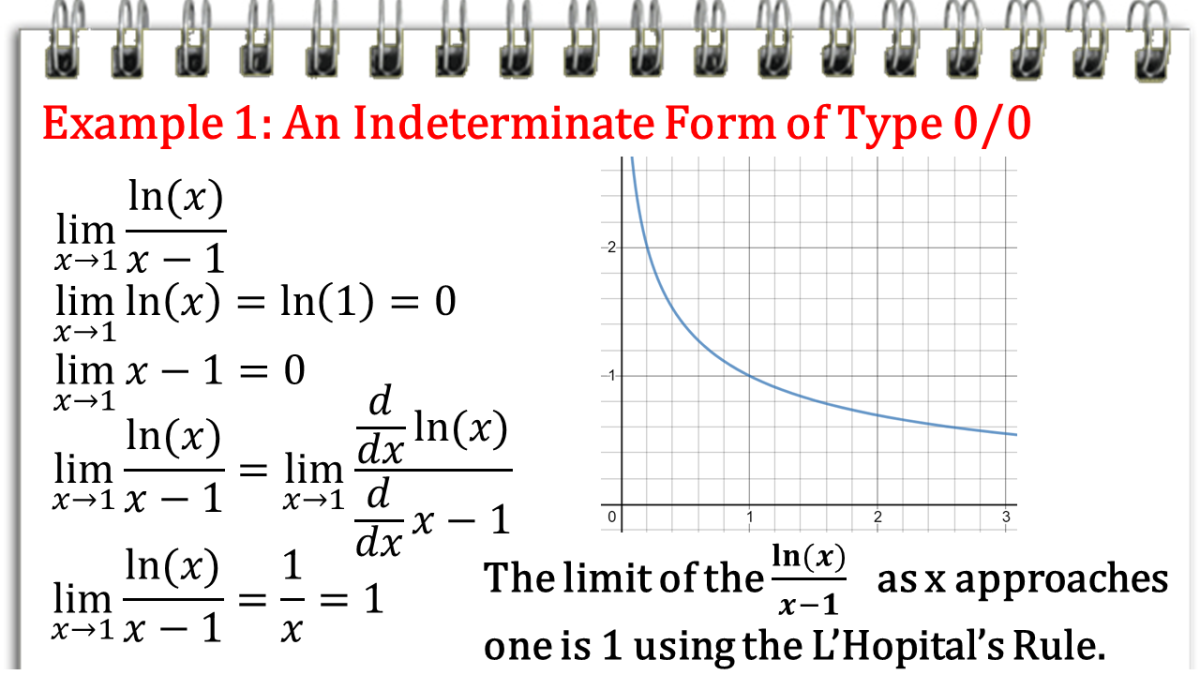



L Hopital S Rule Evaluating Limits Of Indeterminate Forms Owlcation
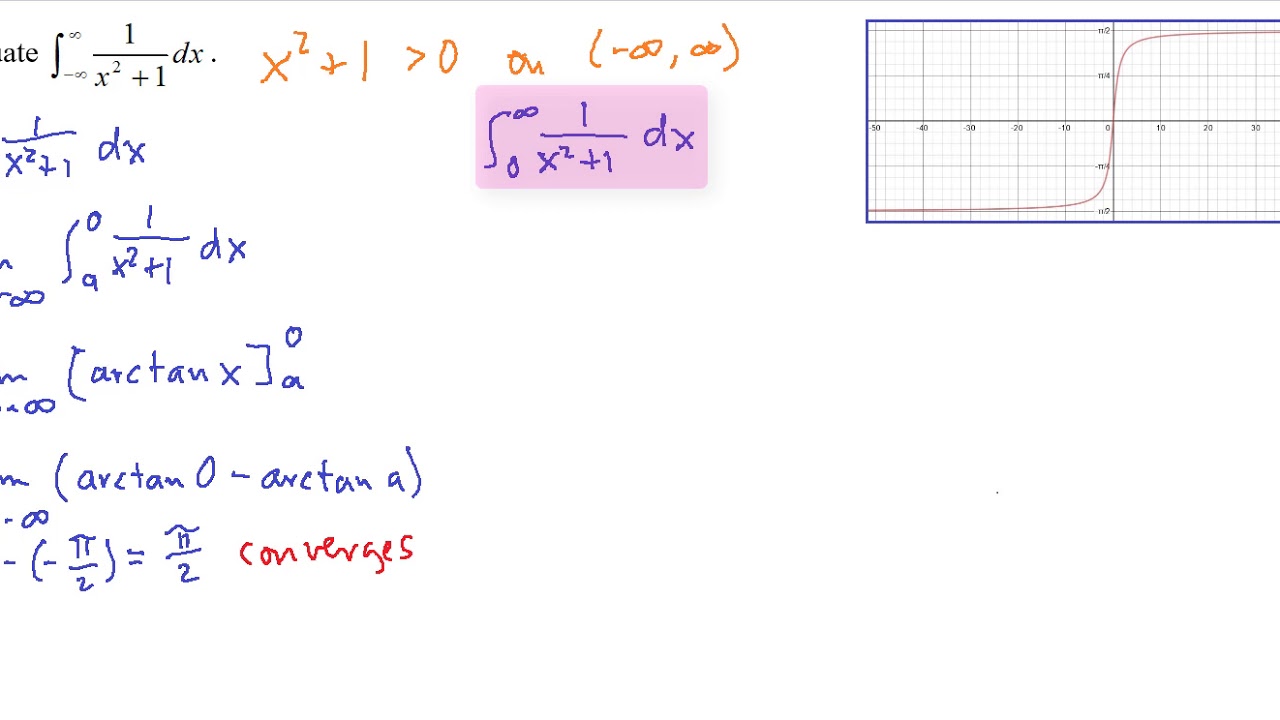



Improper Integrals
The trigonometric function 1 sin x and algebraic function 1 x formed a special function in exponential notation The limit of this special function has to evaluate as x approaches zero in this limit problem lim x → 0 ( 1 sin Let f(x) = {((sinx cosx)cosecx, 1/2 ≤ x < 0), (a, x = 0), ((e^1/x e^2/x e^3/x)/(ae^2/x be^3/x),Lim arctan(1/x) as x>0 Extended Keyboard;
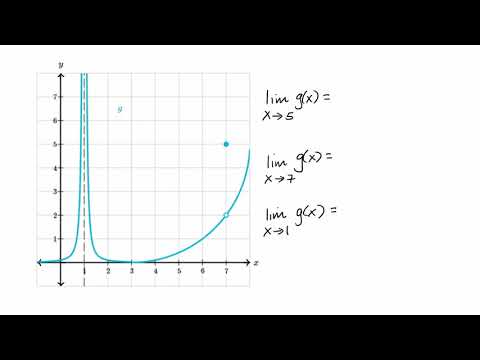



Estimating Limit Values From Graphs Video Khan Academy




Limits
The argument is a little1/x −1/x2 = lim x→0 (−x) = 0 It would have been more correct to omit the last = sign and to say instead therefore lim x→0 xlnx = 0 ; Recalculate the Limit as x approaches 0 for sin (1/x)/ (1/x) and tell me what answer you get The range of sin x is 1,1, so the range of sin (1/x) is also 1,1 Because the limit of x as x→0 = 0, multiplying this by sin (1/x) will give us 0 (because range of sin (1/x) is bounded)



Find The Limit As X Goes To 0 Of 1 X 1 X E X Stumbling Robot




Lesson 18 Indeterminate Forms And L Hopital S Rule
A Also lim x → 0 y = lim x → 0 ( a x – 1) = a 0 – 1 = 1 – 1 = 0 This shows that y → 0 as x → 0 Therefore, the given limit can be written as lim x → 0 Ex 131, 6 Evaluate the Given limit lim┬(x→0) ((x 1)5 −1)/x lim┬(x→0) ((x 1)5 − 1)/x = ((0 1)5 −1)/0 = (15 − 1)/0 = (1 − 1)/0 = 0/0 Since it is of from 0/0 Hence, we simplify lim┬(x→0) ((x 1)5 −1)/x Putting y = x 1 ⇒ x = y – 1 As x → 0 y → 0




Evaluate Limit X Tends To 0 1 X 6 1 1 X 5 1 Maths Limits And Derivatives Meritnation Com




X 1 1 X 1 31 X 2 3 Maths Questions
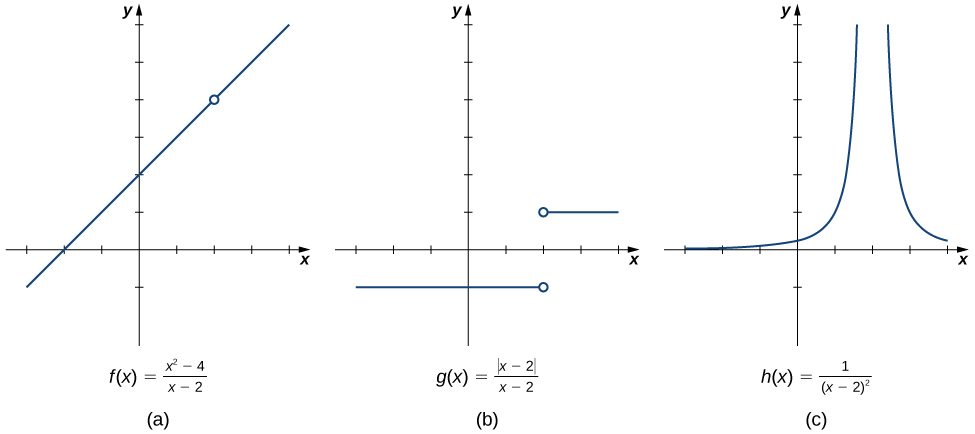



2 2 The Limit Of A Function Calculus Volume 1



Evaluate Lim X 0 1 X 2 Cot 2x Sarthaks Econnect Largest Online Education Community




Limits At Infinity Infinite Limits And Asymptotes




Answered Limits With Trigonometric Functions Bartleby




Lim X 0 1 X 1 3 1 X 1 3 X 2 3
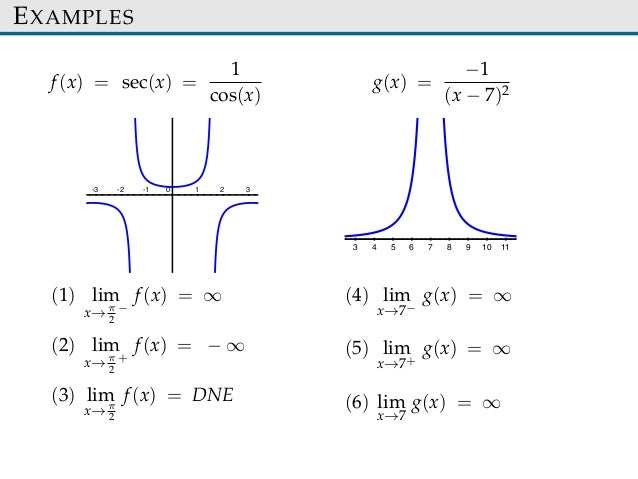



Limite Functions Sect22 24




Ex 13 1 24 Find Lim X 1 Where F X X 2 1 X 1 X 2 1



What Is The Limit Of 1 X As X Approaches 0 Quora




Evaluating Lim Limits X To Pi Frac Pi X Sin X 1 Cos X Mathematics Stack Exchange




Solution Evaluate Lim X 1 X 2 1 X 2 3x 4




Limite Functions Sect22 24



1




One Sided Limits Left Hand Limit And Right Hand Limit Definition Solved Example Problems Mathematics
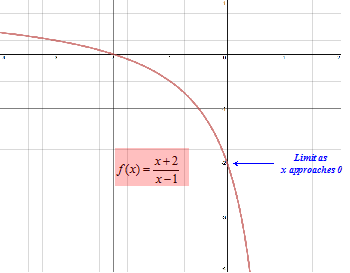



Limits Introduction And One Sided Limits




Ex 13 1 6 Evaluate Lim X 0 X 1 5 1 X Class 11
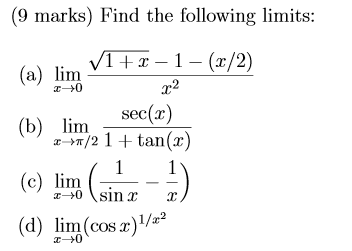



Find The Following Limits A Lim X Tends To 0 Chegg Com




Limits




Solution Evaluate Lim X 0 1 Cos X X




Evaluate The Following Limits X 2 3 2x 2 1 X 2 2




Evaluating Lim Limits X To 0 1 X 1 X Mathematics Stack Exchange
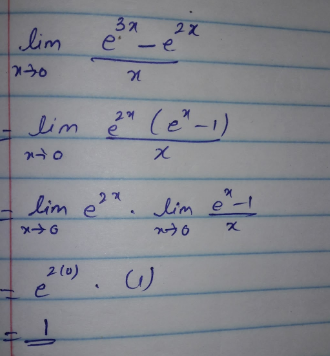



Lim X 0 E 3x E 2x X
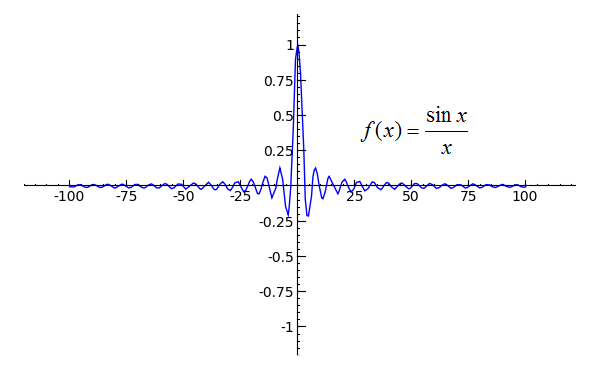



Sage Calculus Tutorial Limits At Infinity



1




Ex 13 1 25 Find Lim X 0 Where F X X X 0 Teachoo



Evaluate Lim X 0 1 3x 2x 2 1 X 1 3x 2x 2 1 X X Sarthaks Econnect Largest Online Education Community



Finding Limits Algebraically




Lim X2 9 X 3 Novocom Top



L Hopital On Limit Of Tanx Lnx As X 0 From The Right Physics Forums
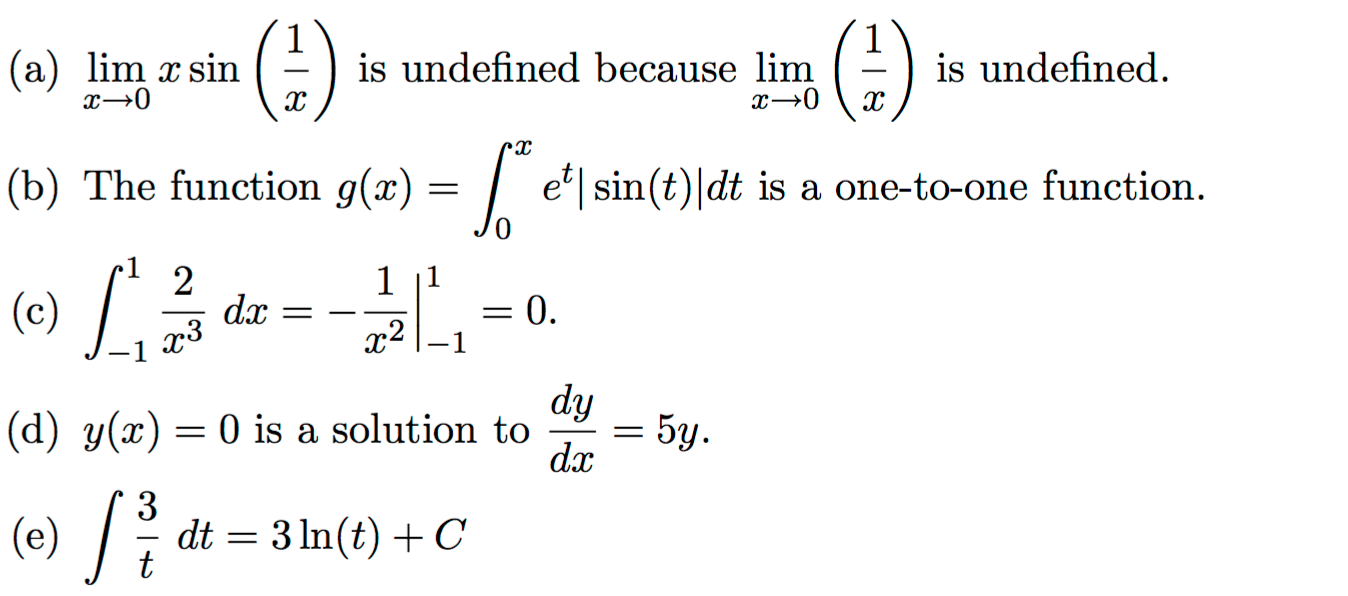



Lim X Right Arrow Xsin 1 X Is Undefined Because Lim Chegg Com




Evaluate X 1x 7 2x 5 1 X 3 3x 2 2




Find Limits Of Composition In The Graph Of F Mathematics Stack Exchange




Limit Of 1 X 1 X As X Approaches 0 Youtube




Limit X Tends To 0 1 X N 1 X Maths Limits And Derivatives Meritnation Com
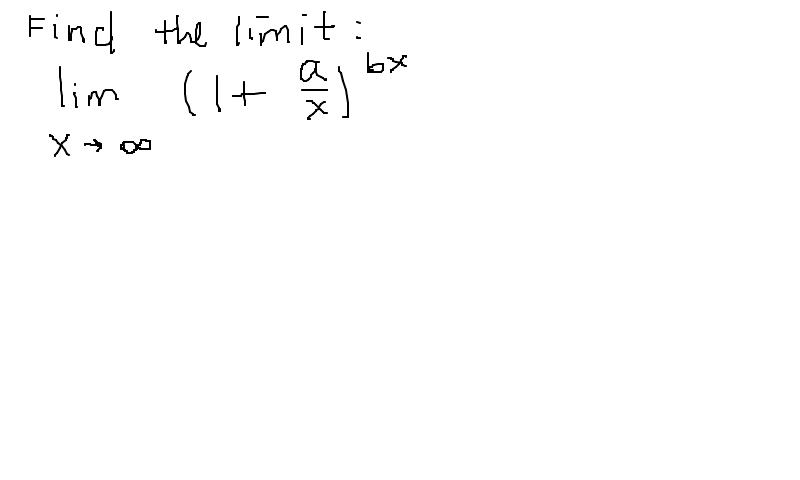



What Is The Limit As X Approaches Infinity Of 1 A X Bx Socratic




Intermediate Forms And L Hospital Rule Ppt Download



What Will Be The Value Of Limit X 0 1 Cosx X 2 Quora
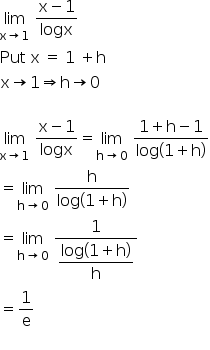



Lim X 1 X 1 Log X Mathematics Topperlearning Com 9gqsqoii



Find The Limit As X Goes To 0 Of 1 X 1 Ex 1 Stumbling Robot
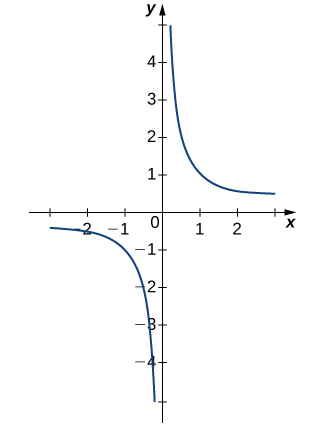



2 2 The Limit Of A Function Calculus Volume 1




Ex 13 1 6 Evaluate Lim X 0 X 1 5 1 X Class 11




Intermediate Forms And L Hospital Rule Ppt Download



12 2 Limits And Continuity Of Multivariable Functions Mathematics Libretexts




Limits By Factoring Video Khan Academy
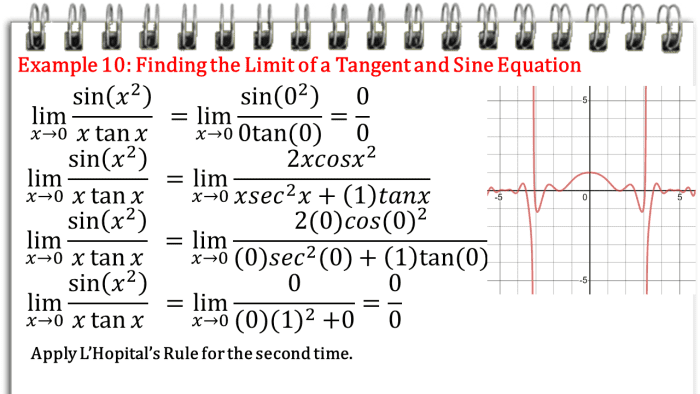



L Hopital S Rule Evaluating Limits Of Indeterminate Forms Owlcation




L Hopital S Rule Evaluating Limits Of Indeterminate Forms Owlcation



Calculus Limits



Evaluate The Given Limit Lim X 0 X 1 5 1 X Sarthaks Econnect Largest Online Education Community



Web Auburn Edu Holmerr 1617 Textbook Limbyalg Screen Pdf
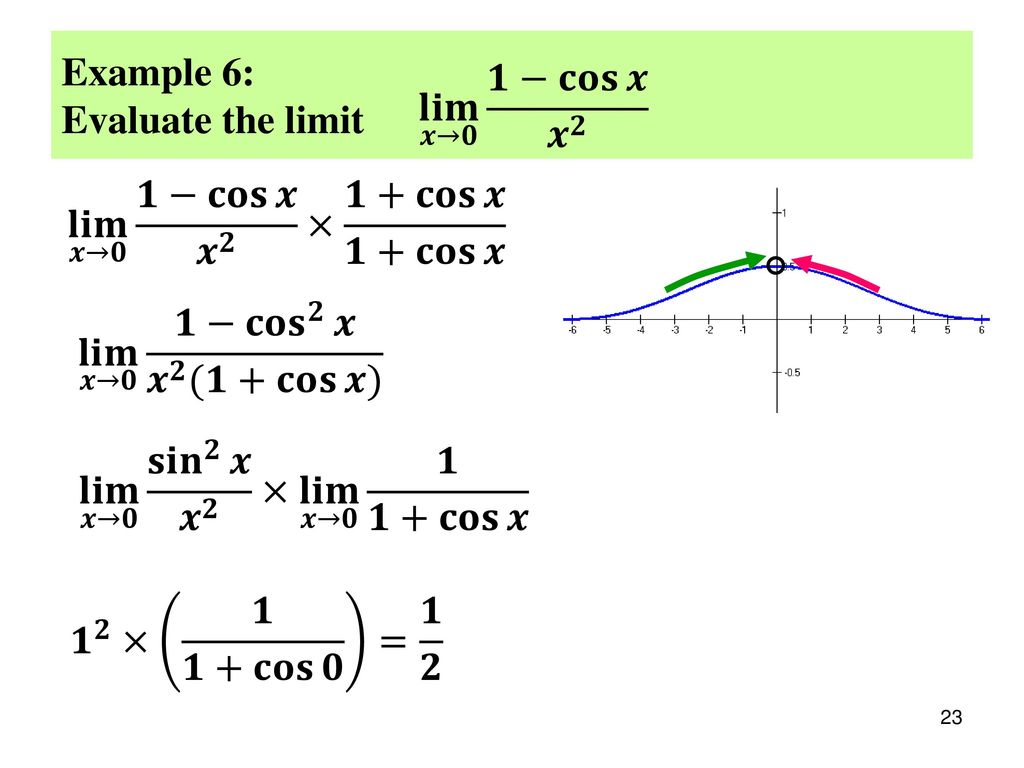



U3 L2 Limits Of Primary Trig Functions Ppt Download
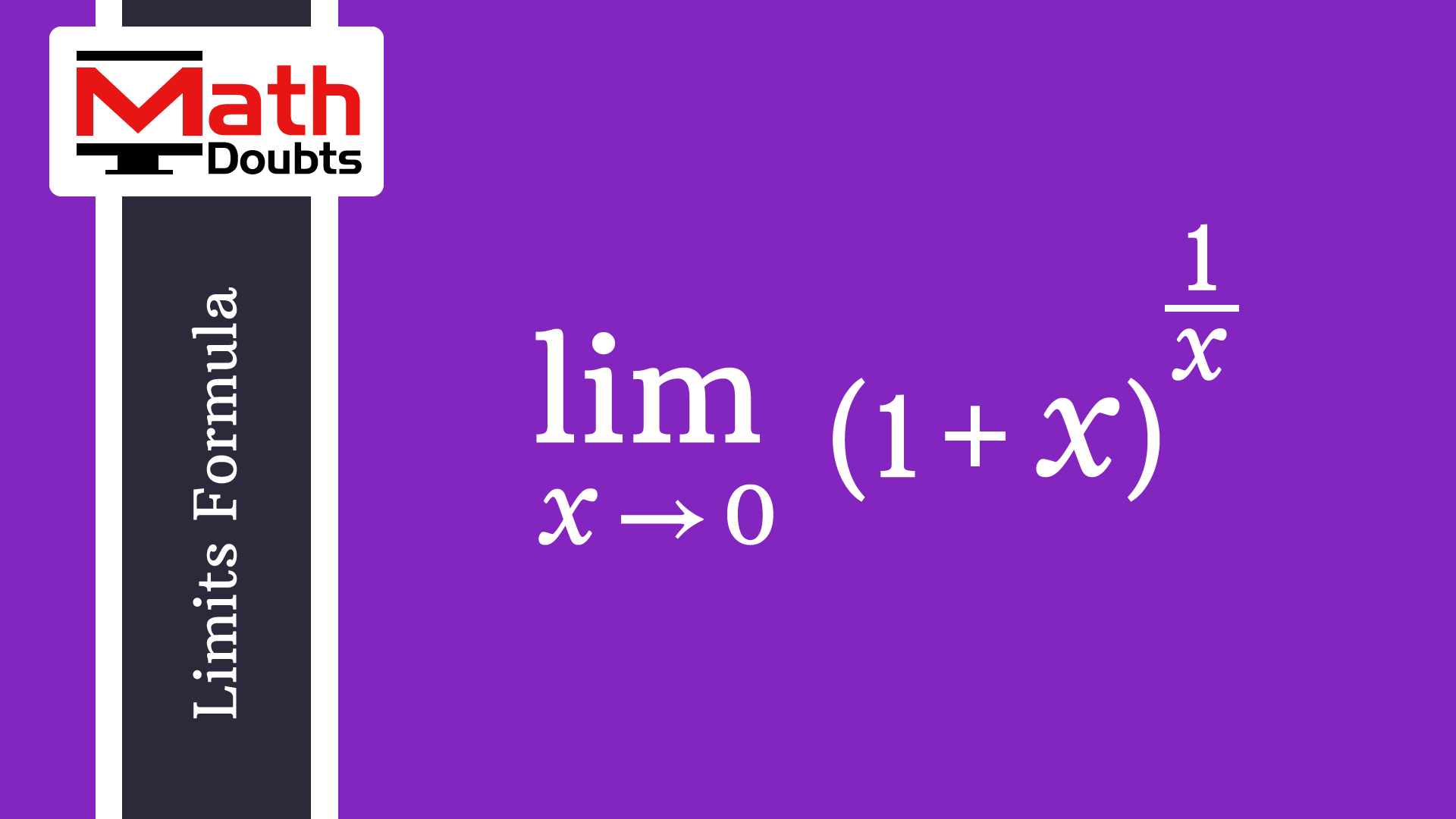



Lim X 0 1 X 1 X Rule




2 5 The Precise Definition Of A Limit Calculus Volume 1




Lim X 0 1 Cos3x X 2 Mathematics Topperlearning Com 2q46hk77



L Hopital On Limit Of Tanx Lnx As X 0 From The Right Physics Forums




Limit Of 1 Cos X X As X Approaches 0 Video Khan Academy




Ex 13 1 6 Evaluate Lim X 0 X 1 5 1 X Class 11



1
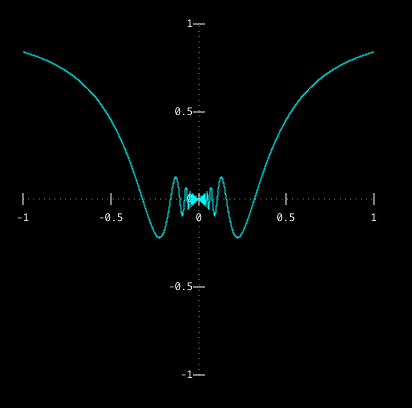



Sin 1 X And X Sin 1 X Limit Examples




Limit Of 1 Cos X X As X Approaches 0 Youtube




How To Determine If A Limit Does Not Exist Video Lesson Transcript Study Com




Finding The Limit Of 1 Cos X X Video Lesson Transcript Study Com




Lim X 0 1 X N 1 X Brainly In



Evaluate Lim X 0 1 X 2 Cot 2x Sarthaks Econnect Largest Online Education Community



Finding Limits Algebraically




Algebra Of Limits Study Material For Iit Jee Askiitians



Find The Limit As X Goes To 0 Of Ax 1 Bx 1 Stumbling Robot




Compute Lim X 0 E 3x 1 X




Limits Of Transendental Function E 1 X 1 E 1 X 1 As X Approaches Zero Test 1 Youtube




Proof Of Limit Of Sin X X 1 As X Approaches 0 Math Linux Com



Calculus Limits




Finding The Limit Of 1 Cos X X Video Lesson Transcript Study Com
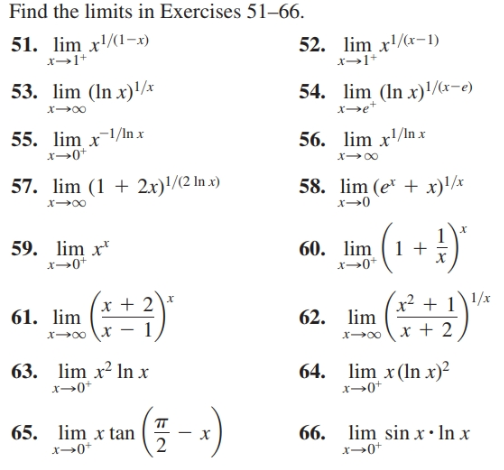



Answered Find The Limits In Exercises 51 66 51 Bartleby




Lim X Tends To 0 1 X 1 X E X Is Equal To Brainly In




Indeterminate Form Wikipedia




How Do You Find The Limit Of Sqrt 1 9x Sqrt 1 8x X As X Approaches 0 Socratic



0 件のコメント:
コメントを投稿