Example 3 Evaluate (i) (𝑙𝑖𝑚)┬(𝑥→1) (𝑥 15 − 1)/(𝑥10 − 1) (𝑙𝑖𝑚)┬(𝑥→1) (𝑥 15 − 1)/(𝑥10 − 1) = (〖(1)〗^15 − 1Lim x → ∞ x 2 x = 1 Für x gegen ∞ strebt der Graph der Funktion gegen 1 Grenzwert für x gegen − ∞ berechnen Wenn die x Werte immer kleiner werden, x − 1 − 10 − 100 − 1000 − f ( x) − 1 0, 8 0, 98 0,998 0,999 8 nähern sich die y Werte der 1 an, d h lim x → − ∞ x 2 x = 1We can also use LHR instead of series expansion for logs and this will require two applications of LHR to get the following expression L = e 6 ⋅ lim x → 0 1 x ( − 1 ( 1 x) 2 4 − x ( 2 − x) 2) = e 6 ⋅ lim x → 0 1 x ( 4 − x) ( 1 x) 2 − ( 2 − x) 2 ( 1 x) 2 ( 2 − x) 2 = e 6 ⋅ lim x → 0 1 x x ( 11 x − x
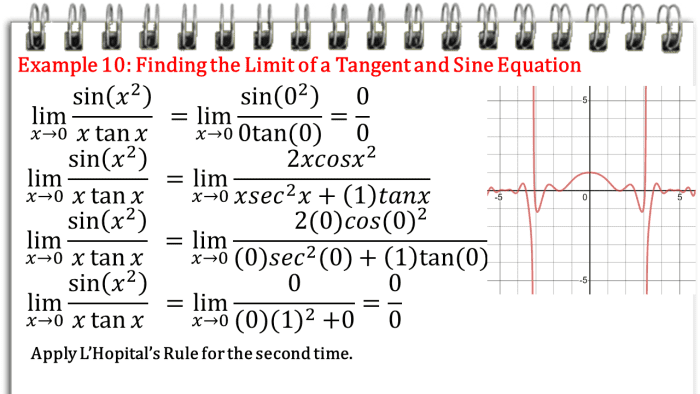
L Hopital S Rule Evaluating Limits Of Indeterminate Forms Owlcation





